There are no developed lesson plans for this activity.
Students will need their Waves on a String Activity Answers from the “Traveling and Standing Waves” Lesson Plan to do this activity.
Learning Goals
Students will be able to:
- Think about waves as a function of time, space or space‐time and explain why waves might be
represented in these different ways. - Define harmonic and determine the relationship between the harmonics.
- Explain the relationship between harmonics and the corresponding wave function.
- Predict what happens when more than one wave is present.
- Apply their understanding about wave characteristics and superposition to match wave functions.
Graphing Waves
- Discuss with your partner how you usually think about waves. Make drawings to help you explain the images in your mind as you try to explain waves.
- Open Fourier‐Making Waves. Investigate how changing amplitude affects the wave. How do your findings compare to your findings from number 3 in the Waves on a String activity? Describe in your own words what the y‐axis for wave graphs represents.
- Change the function of to time(x). Record how the waves compare, the axes labels and which tools change. Then, repeat using function of time and space.
- Which representation does Waves on a String use? (you may need to open Waves on a String again)
- In number 5 in the Waves on a String activity, the graph you made was called vertical position‐horizontal position graph. Summarize how you made the graph. What would you have to do in Fourier‐Making Waves to make a similar graph?
- In number 6 in the Waves on a String activity, the graph you made was called vertical position‐time graph. Summarize how you made the graph. What would you have to do in Fourier‐Making Waves to make a similar graph?
- Use Chapter 14 of your text to see how the author uses different representations of waves to help you understand the definition of a wave.
a. Find a figure that is the function of time. Sketch the figure and record the figure number.
b. Find a figure that is the function of space. Sketch the figure and record the figure number.
c. Read the pages that correspond to these figures. How does the author use each figure to help you understand waves?
d. Why can’t the book represent a wave as a function of space and time? If you were a publisher and wanted to add space‐time representations, what could you do? Describe an event where this format could be used to help the reader.
Harmonics
8. Investigate what harmonics are and describe in your own words what harmonic means.
a. Use the Wavelength tool to determine a mathematical relationship between the wavelengths of each harmonic.
b. Calculate the frequency of the fundamental ‐A1, the second harmonic ‐A2 and the third harmonic ‐ A3.
c. What is the mathematical relationship between the frequencies of all 11 harmonics shown in the sim?
Auditory Perception:
9. Turn on the sound using the “Sound” checkbox.
a. Set all Amplitudes to 1. Can you pick out A5 from this sound? Now try turning A5 to zero and then back up. Now can you hear it? Why do you think this might be?
10. (Taken from “The Science of Sound” 3rd Ed. by Rossing, Moore and Wheeler). Helmholtz demonstrated that the sounds of most musical instruments (including the vocal folds or cords) consist of harmonics that determine the timbre. Furthermore, he carefully described a way in which the ear could comprehend timbre. On the basis of his experiments, he formulated the following general rules:
I. Simple tones, such as those of tuning forks and widely stopped organ pipes, have very soft, pleasant sound, free from roughness but dull at low frequencies.
II. Musical tones with a moderately loud series of harmonics up to the sixth (such as those produced by the piano, the French horn, and the human voice) sound richer and more musical than simple tones, yet remain sweet and soft if the higher harmonics are absent.
III. Tones consisting of only odd harmonics (narrow stopped organ pipes, clarinet) sound hollow and, if many harmonics are present, nasal. When the fundamental predominates, the quality of tone is rich; when the fundamental is not sufficiently strong, the quality of tone is poor.’
IV. Complex tones with strong harmonics above the sixth or seventh are very distinct, but the quality of tone is rough and cutting.
Create a series of investigations using the Harmonics on Fourier: Making Waves to verify the above claims. Describe exactly what you did for each and what you heard. If there are differences in what each lab member heard (which there very likely will be) describe the different perceptions.
Preset Functions:
11. Investigate the different present functions. Describe what each is and how it’s created.
12. Describe what happens to each of the different present functions if you decrease the number of harmonics.
Adding Waves:
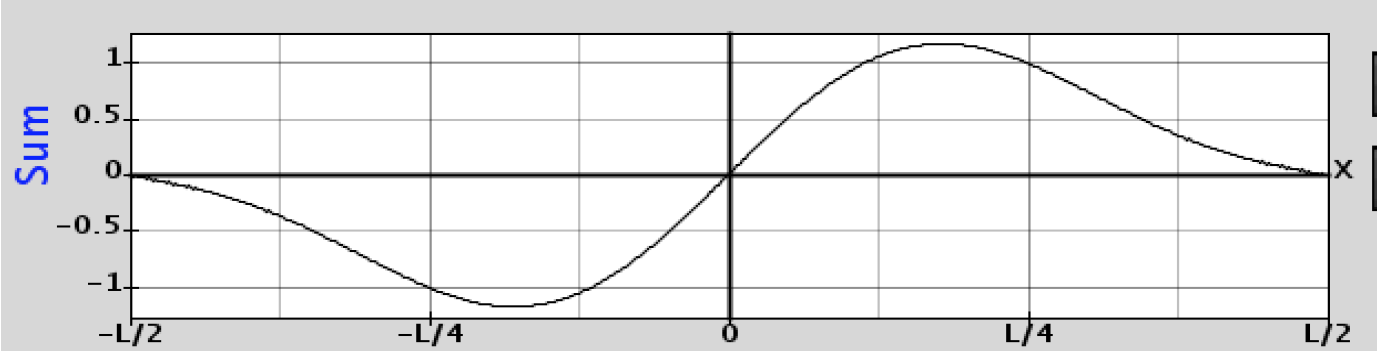
13. Use the simulation to make a Sum Graph that looks like the graph below using only 2 harmonics. It’s important to match both the x and y axes. Print* your Harmonics Graph, record the Amplitudes that you used, and describe what you thought about as you tried to match the graph.
*To print take a screen capture and paste it into another program.
14. Draw what you think the Sum Graph will look like for the harmonics displayed below.
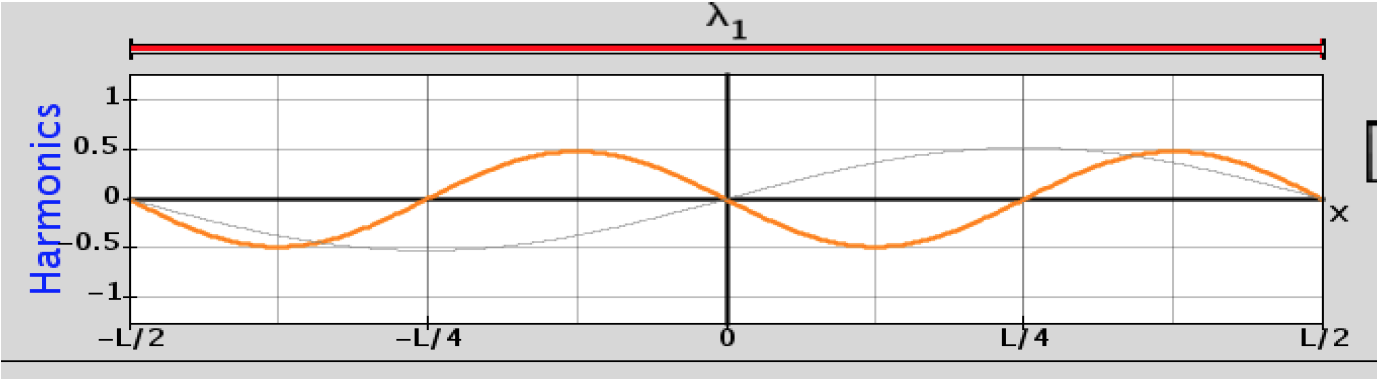
15. Use the simulation to test your prediction and make corrections with a different color pen. Record the amplitudes that you used and write a plan for how you could predict the sum of waves.
16. Use your predictions ideas to draw the sum of these waves.
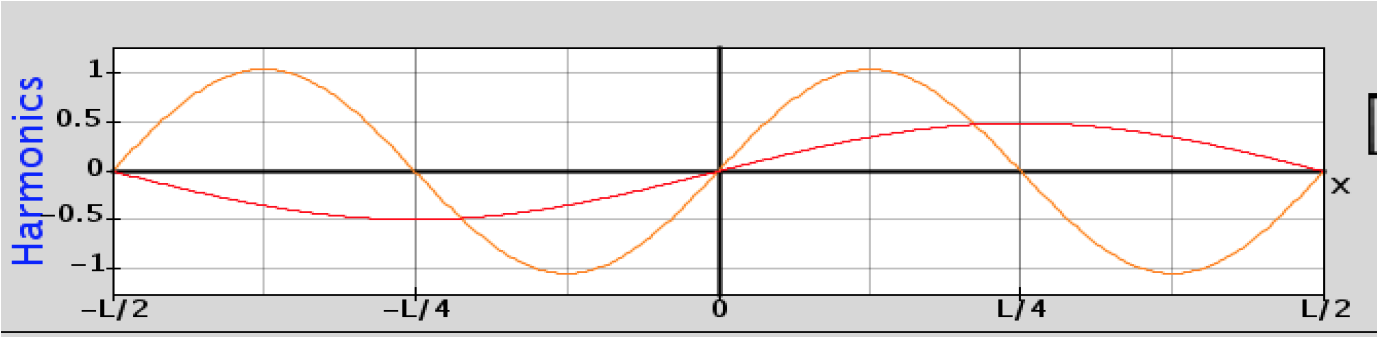
17. Test your ideas using the simulation. Make corrections on the predicted graph with a different color pen. Correct your plans for prediction also.
18. Design a test for your ideas on wave addition. Explain in detail your experiment and the results. Include evidence that your prediction method is repeatable.
Wave Game
Lowest Score Wins!
1. Use the Level 1 for the beginning of the competition. Take turns:
Press New Game, think about what should work, and then type in your guess in the Amplitude box.
Keep score: ‐5 points for correct on first try, ‐3 for second and ‐1 for third.

2. In Level 2, you have to choose one of two harmonics. Take turns:
Press New Game, decide which harmonic to use, think about what should work, and then type in their guess in the Amplitude box.
Keep score: ‐7 points for correct on first try, ‐4 for second and ‐1 for third.

3. In Level 3, you have to choose one of eleven harmonics. Take turns:
Press New Game, decide which harmonic to use, think about what should work, and then type in their guess in the Amplitude box.
Keep score: ‐10 points for correct on first try, ‐5 for second and ‐1 for third.

4. In the other Levels, you have to choose more than one wave to add to make the SUM. Take turns:
Start the stopwatch as the player presses the New Game button. The seconds that it takes to match divided by the level number is the score. Design a spreadsheet to keep track of your scores.
